|
Utiliser Mathematica Bernard Vuilleumier 1. MATHEMATICA S'ADRESSE À TOUS LES ENSEIGNANTS Quel enseignant n'a pas eu à se plaindre de l'incompatibilité fréquente du matériel informatique et du logiciel ? Quel utilisateur n'a pas déploré la difficulté - quand ce n'est l'impossibilité - de réutiliser sur de nouvelles machines, un programme ou un développement qui fonctionnait avec le matériel de la génération précédente ? Vaut-il encore la peine, dans ces conditions, de consentir à des efforts pour apprendre à utiliser un logiciel ? Oui, car il existe actuellement quelques programmes qui fonctionnent sur différentes machines et qui permettent une véritable communication entre leurs utilisateurs, même si ces derniers évoluent dans des mondes très différents et émaillés de rivalités (gros systèmes, stations de travail, ordinateurs personnels). Mathematica est un de ces programmes. Mathematica ne concerne pas que les mathématiciens, il s'adresse à tous les enseignants comme nous allons essayer de le montrer à l'aide de quelques exemples. En histoire Les problèmes de chronologie revêtent une grande importance en histoire. Pour comparer des dates en divers points de la Terre, on recourt à la notion de calendrier. Malheureusement, cette notion n'est pas univoque et elle a beaucoup changé depuis les premières civilisations jusqu'à nos jours. Les calendriers sont basés sur les périodes de rotation de la Terre sur son axe, de la Lune autour de la Terre et de la Terre autour du Soleil. La complexité des calendriers dépend de la façon dont une culture a décidé de tenir compte de ces quantités incommensurables. Les calendriers ont presque tous abandonné une de ces périodes : les calendriers chrétiens ne tiennent pas compte de la lunaison alors que le calendrier musulman utilise une année purement lunaire. Avec Mathematica, vous obtenez facilement les réponses à des questions du type :
Ces réponses peuvent être exprimées dans les calendriers julien, grégorien ou islamique. Par défaut, elles sont données dans le calendrier julien pour des dates allant jusqu'au 2 septembre 1752 (date d'adoption de ce calendrier par les colonies anglaises) puis dans le calendrier grégorien à partir du 14 septembre 1752. Vous pouvez aussi obtenir les réponses à d'autres questions du genre :
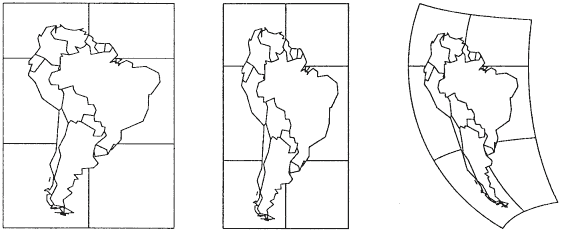
Exemples Q1. Le 5 mars 1798, les Bernois furent battus à Fraubrunnen et au Grauholz par les français. Quel jour de la semaine les Bernois subirent-ils cette défaite ? R1. Les Bernois furent vaincus un lundi. Q2. Le 19 mai 1815 fut signé à Zurich le traité d'union de la République de Genève à la Suisse en tant que 22e canton. Quel jour de la semaine ce traité fut-il signé ? Combien de jours se sont écoulés depuis la défaite des Bernois du 5 mars 1798 jusqu'au rattachement de Genève à la Suisse le 19 mai 1815 ? R2. Le traité fut signé un vendredi. Il s'écoula 6283 jours. Q3. Entre la fin de la guerre civile du Sonderbund marquée par la capitulation du Valais le 29 novembre 1847 et la dissolution de la diète, il s'écoula 298 jours. Quel jour de la semaine le canton du Valais capitula-t-il ? Quel jour de la semaine et à quelle date la diète fut-elle dissoute ? R3. Le Valais capitula un lundi. La diète fut dissoute le vendredi 22 septembre 1848. En géographie Mathematica vous permet d'imprimer toute une série de cartes, de les modifier ou d'en créer de nouvelles. Vous pouvez aussi utiliser le logiciel pour réaliser les différents types de projections utilisés en cartographie (projection équirectangulaire, cylindrique, conique, azimutale, sinusoïdale, de Mollweide ou de Mercator) ou encore pour déterminer la distance entre deux points sur une sphère ou sur un sphéroïde. Exemples Une carte représente une portion de la Terre sur une surface plane. Comme la Terre n'est pas plate, cette représentation nécessite certaines conventions de projection. Ces projections produisent des distorsions. La projection équirectangulaire prend la longitude comme coordonnée x et la latitude comme coordonnée y. Elle ne préserve ni l'aire ni les angles. D'autres projections conservent une propriété de la surface terrestre alors qu'elles en modifient d'autres. Ainsi, par exemple, une projection à aire constante présente la particularité suivante : deux régions de même aire sur la carte ont la même aire sur la Terre. Une projection azimutale conserve les directions depuis un point central.
Fig. 1 : Projections : a) équirectangulaire ; b) à aire constante ; c) azimutale. En biologie Il est possible d'étudier certaines propriétés d'organismes vivants à l'aide de Mathematica en recourant par exemple à la notion d'automate cellulaire. Le plus connu de ces systèmes est l'automate cellulaire à deux dimensions appelé « jeu de la vie » et inventé par John Horton Conway. Imaginez un échiquier infini dont chaque cellule peut prendre, à un instant donné, la couleur blanche ou noire. La règle spécifiant la couleur de chaque cellule au temps t+1 en fonction de l'état des huit cellules adjacentes au temps t est donnée de la manière suivante : 1º si le nombre de cellules vivantes voisinant une cellule vaut 2, cette cellule conserve son état à l'étape suivante 2º si le nombre de cellules vivantes voisinant une cellule vaut 3, cette cellule sera vivante à l'étape suivante, quel que soit sont état présent 3º pour n'importe quel autre nombre de cellules vivantes voisinant une cellule, la cellule sera morte à l'étape suivante. En bref, cette règle exprime qu'une cellule meurt lorsqu'elle est trop isolée ou lorsque son voisinage est trop peuplé. Cet automate cellulaire à deux dimensions permet d'aborder une des questions fondamentales du monde vivant : comment l'auto-reproduction est-elle possible ? Quant à l'auto-organisation, elle peut être mise en évidence à l'aide du cas plus simple d'automates cellulaires à une dimension (figures 2 et 3).
Fig. 2 : Évolution d'une cellule vivante selon trois automates unidimensionnels. L'axe temporel est vertical et pointe vers le bas. La cellule initiale se trouve au sommet de chaque figure. Selon la règle de transition envisagée : a) la cellule initiale se maintient inchangée ; b) elle se duplique pour générer une structure uniforme qui s'étend d'une cellule dans chaque sens à chaque étape ; c) le développement donne lieu à une configuration non triviale.
Fig. 3 : Évolution d'une ligne de cellules dont les états initiaux sont aléatoires. Le fait remarquable est, qu'avec certains automates, l'indépendance des états cellulaires initiaux est complètement perdue et l'évolution fait apparaître une corrélation entre les états : c'est l'auto-organisation. En chimie et en physique En plus de possibilités de calcul - tant numérique que symbolique - et de programmation étendues, Mathematica offre accès à de nombreuses données scientifiques, telles que les constantes chimiques et physiques ainsi qu'aux facteurs de conversion pour passer d'un système d'unités à un autre. Vous trouverez par exemple, pour les éléments chimiques :
En outre, plus de 30 constantes physiques fondamentales sont accessibles, parmi lesquelles :
Vous pourrez exprimer ces grandeurs dans le système international d'unités, dans le système MKS ou dans le système CGS. 2. COMMENT COMMUNIQUER ENTRE UTILISATEURS Supposons que vous enseignez les mathématiques et que vous avez réalisé des exercices à l'aide de Mathematica. Vous êtes naturellement un inconditionnel des micro-ordinateurs qui équipent l'atelier de votre établissement. Un de vos collègues, qui a acquis à titre personnel une machine non compatible avec la vôtre, a également réalisé des exercices avec Mathematica. Malgré vos divergences de vue en matière de matériel informatique, vous partagez les mêmes convictions pédagogiques et vous souhaiteriez échanger vos séries d'exercices. Grâce à Mathematica cela est possible très facilement. En échangeant des disquettes Les fichiers créés sur une machine peuvent être lus et exécutés sur une autre machine, même si elle n'appartient pas au même monde. Il suffit d'enregistrer les fichiers à échanger sur une disquette qui peut être lue par les deux machines et le tour est joué. Et comme les instructions Mathematica occupent très peu de place, une disquette double face par exemple vous permettra d'échanger les exercices correspondant à une année de cours au moins. Par voie télématique La plupart des ateliers est maintenant équipée de façon à pouvoir communiquer avec l'ordinateur du centre informatique pédagogique (serveur du DIP). Vous pouvez donc échanger des fichiers entre ateliers en les déposant sur ce serveur. Si vous possédez un ordinateur et un modem à domicile, vous pouvez également, via ce serveur, communiquer avec les ateliers et avec les collègues qui disposent du matériel nécessaire à la maison.
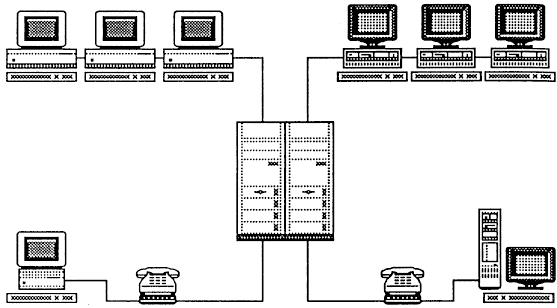
Fig 4 : Le serveur télématique du département de l'instruction publique de Genève (DIP) permet l'échange de fichiers entre ateliers Mac et ateliers PC. Les enseignants qui possèdent un ordinateur et un modem peuvent communiquer entre eux depuis leur domicile. Bernard Vuilleumier Article paru dans Informatique-Information, octobre 1992 - n° 19 Paru dans la Revue de l'EPI n° 71 de septembre 1993. ___________________ |