UN OUTIL POUR "PENSER AVEC"...
Si "comprendre" c'est mettre en relation le schéma de résolution avec une situation problème, si "apprendre", c'est établir des liens entre cette situation problème et le schéma de résolution adéquat, ainsi que le mémoriser pour le retrouver, la géométrie est un lieu idéal pour réfléchir sur les mécanismes de l'apprentissage. C'est en effet un domaine suffisamment formalisé pour que puisse être explicitement mise en place une démarche d'apprentissage de la formalisation qui allie esprit logique et reconnaissance de formes.
C'est dire aussi que la géométrie constitue un domaine idéal pour la recherche en Intelligence Artificielle et en Apprentissage Intelligemment Assisté par Ordinateur.
Le logiciel HYPOTHESES est le fruit d'une telle recherche, théorique et pratique. Encore peu connu, ou, la plupart du temps dans des versions d'approche (la version sous D.O.S., par exemple), il vise non seulement à fournir aux élèves des outils de construction et d’appropriation d’objets géométriques qu’ils ont du mal à concevoir, mais il permet aussi de les mettre dans une véritable situation d'apprentissage. Il vise à les aider particulièrement dans les situations où, devant des situations problèmes, ils ont du mal à identifier le but recherché (la "solution") ainsi que les éléments de départ (les "données"), éléments indispensables à la mise au point d'une méthode de résolution.
En effet, la plupart des élèves - au moins au collège, mais c'est encore vrai au lycée - ont d'abord du mal à identifier "ce qu'on leur demande". Faute de cette boussole, ils ne peuvent repérer les éléments dont ils disposent pour répondre à la question et travaillent - quand ils travaillent - au hasard, pour "faire plaisir" au professeur - ou avoir la paix -, et non pour "apprendre quelque chose".
Une fois identifié "ce qu'on leur demande", si les difficultés de la langue n’ont pas été insurmontables, ils ont encore du mal à repérer les éléments (données ou théorèmes) dont ils disposent, à discriminer les informations pertinentes, c'est à dire les données qui correspondent au problème posé. Autant dire que l’activité qui leur est proposée n’a, dans ces conditions, aucun sens à leurs yeux.
L'inconvénient des situations traditionnelles est qu'on ne peut pas mettre un professeur à tout moment derrière chaque élève. Avec HYPOTHESES, cet inconvénient est en grande partie levé, dans la mesure où, contrairement à ce qui se passe sur le papier, l'élève peut "essayer" des solutions successives - tant en construction qu'en démonstration - dans un effort de modélisation et s'appuyer sur les capacités de simulation de l'ordinateur : si sa solution ne convient pas, l'ordinateur le lui dit. Il lui explique même pourquoi sa solution ne convient pas, par exemple si cette solution s'appuie sur un théorème non démontré.
C'est donc pour contribuer à un véritable dialogue qu’a été construit HYPOTHESES, au fil des années, en fonction des demandes d'enseignants "du terrain" et des observations faites au quotidien dans l'utilisation qu'en font les élèves. C’est cette observation et ces demandes qui nourrissent les bases de connaissances... pédagogiques du logiciel .
On trouvera ci-dessous le témoignage de deux collègues, professeurs de mathématiques, l’un au lycée, l’autre au collège, qui ont eu l’occasion d’expérimenter HYPOTHESES avec leurs élèves.
I. Le point de vue d'un professeur en lycée.
Bernard Montuelle - Professeur au Lycée Giraux Sannier - 62 Saint-Martin-les-Boulogne.
De la construction à la simulation.
Ce qui a surtout retenu mon attention, avec HYPOTHESES, c'est qu'il ne s'agit pas d'un logiciel de dessin, même géométrique, mais d'un logiciel de construction. En effet, l'utilisateur construit sa figure au sens mathématique du terme : en définissant rigoureusement chaque objet géométrique par ses propriétés et en lui donnant un nom. Tous les objets créés ne sont en effet connus du système comme de l'élève, que par leurs noms.
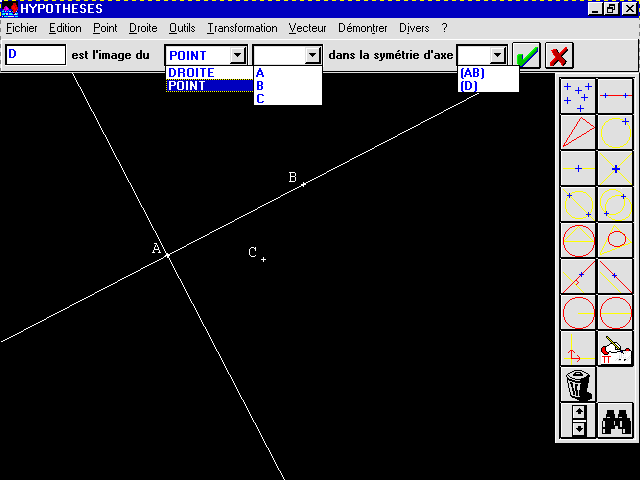
Sur le plan pratique, les noms d'objets élémentaires (point, segment, droite, cercle, etc.) peuvent être choisis dans un menu à l'aide d'un simple clic de souris. Mais, et c'est là une caractéristique intéressante du logiciel : il n'est pas question de créer ainsi un objet, tel qu'un segment, si les éléments qui le constituent n'ont pas été définis préalablement : pas question de créer un "segment [ab]" si les points A et B n'ont pas été définis et positionnés au préalable. Pas question de créer un cercle de centre o et de rayon r si le point o n'a pas été déjà défini. Dans le cas d'une telle tentative, le système intervient pour dire qu'il n'a pas assez d'éléments pour construire la figure. HYPOTHESES, dans ces conditions, est une véritable école de rigueur.
Une fois choisi le type d'objet à créer, automatiquement apparaît une phrase à compléter, correspondant aux caractéristiques de l'objet choisi : l'utilisateur n'a plus qu'à compléter cette phrase en sélectionnant dans des listes déroulantes les noms des objets existants qui le constituent. Aux yeux de l'élève, et particulièrement à ceux qui "manquent de méthode", est ainsi mise en évidence une démarche de travail systématique, à la fois simple et rigoureuse.
Tous les objets de la géométrie plane sont accessibles (du milieu au barycentre en passant par le cercle inscrit, la bissectrice, etc.). Le logiciel prend en compte les vecteurs en permettant de réaliser sur eux des opérations telles que : somme, produit par un réel, produit scalaire.... Les transformations du plan (isométries, projection, homothétie) peuvent être appliquées à de nombreux objets (points, droites, cercles, triangles ...), elles peuvent aussi être nommées ou même composées.
HYPOTHESES autorise aussi une exploration analytique : un point peut être défini par ses coordonnées, une droite définie par son équation et, un repère étant donné, l'éditeur permet la visualisation des coordonnées des points, des vecteurs ainsi que des équations des droites. Enfin, l'éditeur algébrique permet, entre autres, de définir des fonctions dont on peut faire tracer la représentation graphique.
Les figures sont construites à partir de points quelconques (points "libres") et éventuellement de variables numériques. Le logiciel, gérant les propriétés liant tous les éléments de la figure, reconstruit immédiatement et automatiquement la figure dès qu'un point libre est déplacé (pas d'accès à un menu spécial, la souris reconnaît les points déplaçables et change de pointeur au moment où elle passe dessus). La multiplication des études de cas est donc rendue possible, extrêmement aisée, et facilite, du point de vue de l'élève, une démarche de recherche qui serait beaucoup plus difficile, sinon quasiment impossible à réaliser sans l'ordinateur.
Cette capacité à multiplier les études de cas est renforcée par la possibilité de reconstruire la figure en modifiant le contenu des variables dont elle dépend (là aussi c'est la souris qui travaille : pas d'affectations successives et pénibles à la main !). Bien sûr, ces "déformations" peuvent s'accompagner d'études de lieu, d'affichage de la valeur de certains paramètres (angles, distances, valeurs calculées en fonction d'autres nombres ou mesures). Mais HYPOTHESES peut aussi construire la courbe représentative des variations d'un paramètre en fonction de celui qui provoque la déformation de la figure : il est ainsi possible de mettre en évidence, par exemple, la présence d'extremums.
On voit que toutes ces possibilités permettent à l'élève de faire ses expériences sans être "bloqué" par l'usage des instruments de dessin, mais aussi en lui fournissant à la fois, de façon très souple, de nombreux moyens d'exploration et les outils d'une rigueur indispensable en géométrie.
Ces facilités sont bien sûr, exploitables par l'enseignant qui dispose là d'un outil permettant d'animer facilement les figures qu'il veut utiliser comme support de cours : déformations, conséquences numériques.... Ceci avec d'autant plus d'évidence qu'HYPOTHESES permet, en une seule fenêtre, de travailler l'aspect des objets construits : couleur, type de trait, etc. On voit tout l'intérêt d'un tel outil manipulé en public, avec une tablette de rétroprojection ou un écran géant.
Pendant qu'il est question du "confort" de l'enseignant, signalons la possibilité d'imprimer les figures avec la qualité "traceur" sur n'importe quelle imprimante (pas de droites en escalier, figure respectant rigoureusement les dimensions fixées par l'utilisateur). Notons enfin qu'il est possible d'"exporter" ces figures, avec cette même qualité de tracé, vers un traitement de textes.
Me consacrant ici à la géométrie, je ne parlerai pas de l'intéressant analyseur algébrique, préférant passer directement de la construction à la démonstration.
De la construction à l'exercice sous contrôle.
HYPOTHESES permet donc de travailler librement et de libérer une riche imagination dans le domaine de la géométrie (trouver et résoudre des problèmes...). Mais il peut aussi être plus "contraignant", ce qui ne veut pas dire moins intéressant, en devenant "exerciseur".
Au chargement de l'exercice, l'élève se voit proposer l'énoncé correspondant à l'énoncé choisi. Mais il n'est pas purement et simplement livré à lui-même. L'énoncé est couplé à un hypertexte multimédia : les mots de l'énoncé appartenant au dictionnaire sont autant de boutons auxquels sont associées des explications. A chaque mot du dictionnaire est attachée une image (figure, schéma ou autre...), un texte et parfois même un son ou une séquence vidéo. Certains mots du texte peuvent à leur tour évoquer matériellement pour l'utilisateur une autre "page" du dictionnaire. Tout au long de l'activité, l'élève pour faciliter sa recherche, peut consulter, dès qu'il le veut, l'énoncé ou le dictionnaire.
Et si le professeur n'est pas entièrement satisfait des définitions proposées, qu'il ne trouve pas assez adaptées à ses élèves ? La réponses est agréable à entendre : le professeur peut modifier tous les éléments du dictionnaire en ligne mis à la disposition de l'élève, et ceci très aisément.
L'énoncé ayant été lu et étudié à l'aide des outils proposés, l'élève peut commencer son travail. A partir de ce moment, il n'est pas livré à lui-même :le système expert d'HYPOTHESES est activé et se tient prêt à intervenir pour l'aider. De quelle façon ? Au fur et à mesure de la construction, la machine compare la figure de l'élève avec celle du professeur qui a conçu l'exercice. Si une erreur est commise, la machine envoie un message qui a été écrit par le concepteur même de l'exercice. Si le concepteur de l'exercice le désire, des suggestions, des messages d'aide, peuvent être envoyées à l'élève en fonction de la situation. Enfin, lorsque l'exercice est réussi un message prévient l'utilisateur.
On a compris que si le logiciel HYPOTHESES est livré avec une banque d'exercices, chaque professeur peut lui-même créer les exercices qu'il peut lui sembler bon de créer pour ses élèves.
Ce qu'il faut comprendre ici, c'est que si le système-expert est mis à la disposition de l'élève et du professeur pour contrôler et, s'il le faut, guider l'élève, le contenu pédagogique d'un exercice est sous la responsabilité complète de son concepteur, dont la liberté est entièrement préservée. On pourrait penser que des connaissances informatiques "pointues" sont nécessaires à cette conception. Il n'en est rien ! Très souvent, il suffira de construire soi-même la figure attendue pour que la machine se "débrouille" seule pour en faire un exercice ! Pour "fignoler", il restera à saisir les messages d'erreurs et d'aide et d'indiquer par un simple clic, quelles fonctions sont interdites à l'élève pendant cet exercice. En effet, faire construire un parallélogramme en laissant ou en enlevant le menu "parallèle" change complètement la finalité d'un exercice.
De la construction à la démonstration guidée et corrigée par la machine.
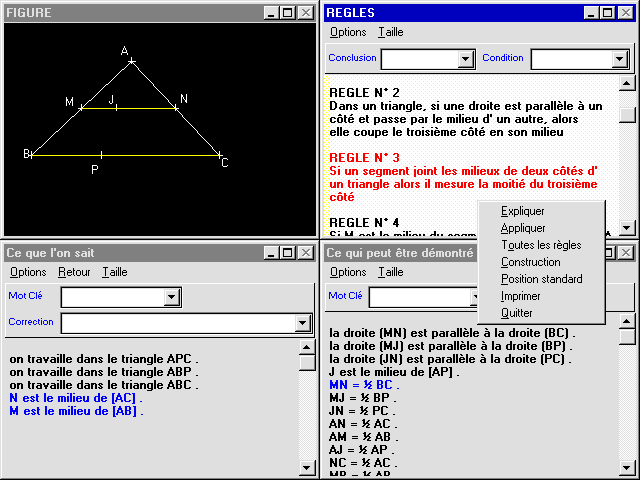
Si le concepteur le désire, la construction peut se poursuivre par un exercice de démonstration portant sur la figure construite. A ce moment là, l'élève "bascule" dans un autre écran composé de 4 fenêtres : la première contient sa propre figure, la suivante contient les théorèmes pouvant être utilisés dans cet exercice, les deux dernières rassemblent, l'une, les hypothèses dont il dispose et l'autre les conclusions à prouver.
Pour réaliser un pas de démonstration, l'élève sélectionne donc les hypothèses nécessaires, la conclusion à laquelle il pense parvenir et le théorème qui lui permet d'y arriver. Au fur et à mesure de ces sélections, la machine colorie les éléments concernés de la figure. Si le pas de démonstration est correct, la machine le signale de façon particulièrement démonstrative en transportant l'assertion démontrée de la fenêtre "conclusions" à la fenêtre "hypothèses". Si ce n'est pas le cas, un message lui explique d'où vient l'erreur : hypothèses insuffisantes ; hypothèse, théorème et conclusion incompatibles ; hypothèse non encore démontrée......). A tout moment, l'élève peut retourner dans le module de construction pour modifier sa figure ou demander à se faire expliquer les théorèmes à utiliser dans le contexte de l'exercice (appui graphique dans sa propre figure).
Dans ce cas aussi, le concepteur de l'exercice est entièrement responsable du contenu : choix du problème bien sûr, mais aussi choix des théorèmes fournis ou à trouver, ainsi que leur libellé.
Il faut souligner que ces définitions se font en langage naturel et que, pour faciliter la "prise en main" de la création des exercices, les exercices fournis avec le logiciel peuvent être facilement modifiés dans tous leurs éléments : énoncés, théorèmes, etc.
En conclusion, pour moi, HYPOTHESES est un logiciel dont l'intérêt tient à ses qualités mathématiques, à ses qualités ergonomiques et surtout... pédagogiques. Un logiciel pour des enseignants qui aiment la géométrie, et pour des élèves qui l'aimeront !

II. Le point de vue d'un professeur en collège.
Danièle Fosseux - Collège R. Salengro - 62 Saint-Martin-les-Boulogne.
Pourquoi j’ai été séduite par "Hypothèses" ?
Depuis longtemps j'utilise des logiciels dans le cadre de mes cours de mathématiques. J’en ai utilisé, et j'en utilise encore plusieurs, de diverses sortes, de façon à faire face à différents besoins ; mais, progressivement je me suis mise à utiliser de plus en plus, et de façon privilégiée, HYPOTHESES, pour la géométrie, avec mes élèves du collège, de la sixième à la troisième. Pourquoi ? Il m’est apparu très vite une différence fondamentale avec la plupart des autres logiciels, qui sont surtout utiles comme outils pour que le professeur montre aux élèves les éléments qu’il souhaite voir compris, à la tablette de rétroprojection ou sur grand écran. La différence, avec HYPOTHESES, c’est qu’il s’agit d’un logiciel essentiellement pensé pour un emploi par les élèves. Cela s’explique dans la mesure où le coeur du logiciel repose sur un système-expert, capable non seulement de réaliser les constructions ou les démonstrations demandées, mais aussi d’intervenir sur le travail de l’élève.
Ces qualités du logiciel font du professeur un observateur privilégié de la démarche de l’élève, de ses gestes d’apprentissage, ce qui n’est pas toujours facile à réaliser autrement, en classe. A partir de ces observations, je peux ajuster mon enseignement, diversifier mes explications et les exercices non pas en fonction de la seule logique disciplinaire - quoiqu'elle soit toujours présente et respectée - mais, réellement, en fonction de chaque élève.
Exemples d’utilisation.
La façon de guider le travail de l’élève sur machine dépend essentiellement du niveau du groupe et de son " hétérogénéité ". Chaque élève travaille seul. La classe est divisée en deux groupes, l’un travaille sur machine tandis que l’autre travaille sur fiche, très souvent sur la rédaction du scénario de construction de l’exercice précédemment fait avec confrontation des différentes stratégies ou à la rédaction de la démonstration du problème recherché.
La prise en mains du logiciel a nécessité la plupart du temps deux séances d’une heure pendant laquelle les élèves ont été guidés, sur des constructions élémentaires, pour réfléchir suivant leur niveau de connaissance à l’aspect axiomatique de l’objet à construire. Exemples :
· Construire une droite : la phrase inscrite à l’écran par le logiciel doit être complétée par le choix des deux points qui la détermine, or au départ l’élève ne construit pas de points....
· Créer l’intersection de deux cercles. Les élèves " voient " les intersections et " posent " les points, mais ne sentent pas la relation derrière les objets.
Voici deux exemples de séances.
a) Le premier est un exemple en construction en classe de cinquième (2ème trimestre) :
En chargeant l’exercice l’élève lit l’énoncé dans lequel les mots losange et diagonale apparaissent en jaune, ils appartiennent au dictionnaire hypertexte associé, une définition et une figure peuvent donc être consultées. Cet exercice possède un modèle, c’est à dire la figure faite et codée, modèle que l’élève peut rappeler à chaque instant. Enfin sur l’écran les points A et C sont donnés, aucun outil de base n’a été inhibé.
A priori à cette période de l’année la classe est autonome et je laisse le groupe démarrer sans aide. Seuls, "losange" et la mesure de BD étant vérifiés par le système, les élèves ont toute latitude pour développer leur propre stratégie de construction.
Pour deux élèves, dans une séance récente qui fait pour moi référence, j’ai du intervenir afin de les aider à se poser les questions " qu’est-ce qu’un losange, quelles sont les propriétés des diagonales, que représentent les points construits ...etc.
Le dynamisme de la figure permet à la plupart d’entre eux de vérifier si celle-ci conserve ses propriétés, mais quelques-uns ont encore du mal à rectifier leur erreur bien qu’ils l’aient découverte et que le système l’ait signalée (création de l’intersection de deux objets, placer un point sur un objet), le plus souvent un camarade guide.
b) Le second exemple concerne une activité de démonstration.
Le logiciel est livré avec un certain nombre d’exercices par niveau mais il m’arrive souvent de créer les miens propres.
En Cinquième le travail sur machine est régulier, sur 15 jours la classe en deux groupes a fait selon le cas un ou deux exercices. Le but premier est la découverte du lien entre données, règles et conclusion avec progressivement des pas croissants de démonstration.
En Quatrième le travail sur machine est beaucoup moins régulier, programme oblige. Outre le but précédent qui est poursuivi, les élèves utilisent le logiciel pour " chercher un problème compliqué ou faire la correction d’un problème pas du tout compris ". Enfin pour des élèves peu doués en géométrie, construire une figure complète de façon que les hypothèses soient toutes disponibles et demander à chaque pas l’explication d’une règle dans le contexte de l’énoncé les aident à choisir les bonnes hypothèses en regard de la conclusion souhaitée.
Le système ne donne une autre stratégie que si elle est plus courte que celle de l’élève ou égale en nombre de pas et seulement si celui-ci a atteint le but prévu. (Et bien entendu si le professeur a donné au système les théorèmes nécessaires).
Exemple :
ABC est un triangle isocèle en A. on appelle D le symétrique de B par rapport à A. Démontrer que le triangle BCD est rectangle en B.
Les deux propriétés cercle circonscrit et médiane ont été introduites dans la base.(Si les élèves sont assez avancés dans leur apprentissage j’introduis dans la base théorèmes directs et réciproques de manière à obliger l’élève à un choix raisonné).
En une première étape l’élève construit la figure (vérifiée par le système).
En une seconde étape il va raisonner sur SA figure EXACTE en ayant à sa disposition :
- les données complètes, si la figure est elle-même complète ;
- toutes les conclusions possibles, et enfin,
- les règles mises à sa disposition.
Les données qu’il sélectionne apparaissent en couleur sur la figure de façon à insister sur le lien entre les deux, c’est au début un sujet d’étonnement.
Autres sujets d’étonnement : le système met le doigt sur l’erreur, ne la corrige pas mais justifie son intervention : " il y trop d’hypothèses pour démontrer que " ou au contraire pas assez, ou bien celles choisies ne permettent pas de conclure. Si l’élève choisit seulement la règle le système l’explique dans le contexte de l’énoncé.
Réaction d'un élève : " On peut démontrer tout ça ? ? et vous ne nous le demandez pas....!"
Au moment du bilan le système est capable de dire à l’élève que certains pas de raisonnement qu'il a faits sont justes mais pas utiles pour le but poursuivi. C'est parfois dérangeant pour l’élève, mais c'est l'occasion pour lui de l'amorce d'une réflexion métacognitive...
Un regret, les règles peuvent être choisies par mot-clé dans les hypothèses ou les conclusions, mais peu d’élèves utilisent cette " facilité " en phase d’apprentissage. En revanche, ils complètent volontiers la figure si certains éléments qui leur semblent utiles n’ont pas été demandés explicitement par le système.
Ils ne font appel à moi que lorsqu’ils ne s’en "sortent pas du tout", en dernier recours.
Conclusion : de la remotivation à de réels apprentissages.
Avec l’emploi d’Hypothèses, j’ai pu constater des effets intéressants.
D’abord, et ce n’est pas négligeable, j’ai pu constater une évolution de l’attitude des élèves. Au début de l’année, il viennent faire de la géométrie en reculant... même sur ordinateur, et progressivement, leur attitude change, ils se mettent à s’intéresser, et, dans la mesure où ils réussissent enfin quelque chose, la plupart y prennent goût et se mettent à faire volontiers de la géométrie.
Au bout d'un moment j’ai pu constater que les élèves commencent à se poser de vraies questions, ils ne font plus des essais désordonnés guidés par la pure fantaisie ; même les moins intéressés ne se contentent plus d'écrire une solution sur le papier, n'importe laquelle, pour avoir l'air d'avoir fait quelque chose et se débarrasser du devoir sans avoir vraiment travaillé ; ils prennent aussi l'habitude de regarder "ce qu'ils ont", c'est à dire de prendre en compte de façon exacte les données du problèmes
Progressivement, ils comprennent mieux le sens des théorèmes : ils voient enfin que c’est le lieu du passage entre les données du problème et la solution. Lorsque la machine leur dit " avec la règle (théorème) que tu as choisi, je ne peux pas prouver que... " ça leur saute en pleine figure....Mais il y a un point sur lequel j'ai pu observer une réelle amélioration, c'est le changement de statut d'une conclusion partielle une fois qu'on l'a trouvée et qu'elle a été vérifiée. " Mais alors, je peux la réutiliser... " m’a dit un jour un élève de quatrième. La plupart des élèves ne comprennent pas bien cela, ils ne comprennent pas facilement qu'on progresse dans le raisonnement, et qu'on s'appuie sur ce qui vient d'être trouvé. Dans HYPOTHESES, le fait qu'une conclusion prouvée passe au rang des "HYPOTHESES" se voit à l'écran. La conclusion passe physiquement d'une zone de l'écran à l'autre, de la liste de ce qu'on a à prouver à la liste des données sur lesquelles on peut s'appuyer...
A long terme, les professeurs qui ont eu ces élèves après moi me disent que les élèves concernés ont compris deux choses : que pour résoudre un problème de géométrie, il faut savoir où on va (quelle est la conclusion cherchée), ce qu'on a au départ, et qu'à chaque pas de démonstration on doit avoir hypothèses / théorèmes / conclusion. Toujours sur le long terme, j'ai eu des élèves qui ont demandé à venir au "club math" l'année d'après pour "faire des problèmes sur l'ordinateur". De toute évidence ces élèves n'auraient pas fait cette démarche s'il n'y avait pas l'ordinateur, et le logiciel HYPOTHESES qui va avec.
Jacques GRESSIER
Bernard MONTUELLE
Danièle FOSSEUX
Article paru dans la Revue de l'EPI n° 85, mars 1997.